Normal distribution is a foundational concept in statistics, characterized by its bell-shaped curve. In this article, we will explore the intricacies of normal distribution, particularly focusing on a mean of 9.75 meters per second and the implications of its standard deviation. Understanding these concepts is crucial for various fields, including psychology, finance, and natural sciences.
In the realm of statistics, the normal distribution serves as the basis for many statistical theories and applications. It is essential for researchers and professionals to grasp how the mean and standard deviation define the distribution's characteristics. This article will break down these ideas into understandable segments and provide insightful examples to illustrate their importance.
As we delve deeper into the world of normal distribution, we will examine its applications, the significance of the mean and standard deviation, and how they can be utilized effectively. By the end of this article, you will possess a comprehensive understanding of normal distribution with a focus on practical applications. Let’s embark on this statistical journey!
Table of Contents
What is Normal Distribution?
Normal distribution, often referred to as the Gaussian distribution, is a probability distribution that is symmetric about the mean. This means that most of the observations cluster around the central peak, and the probabilities for values further away from the mean taper off equally in both directions.
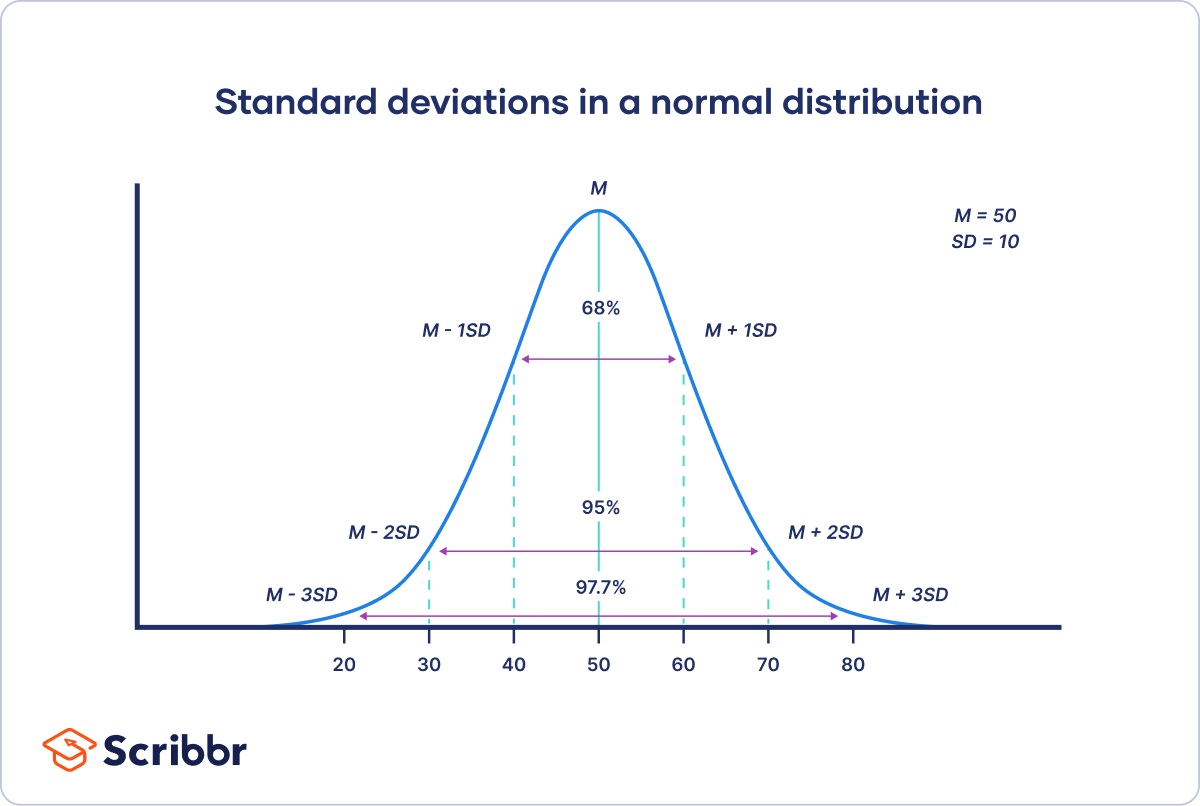
The normal distribution is defined by two parameters: the mean (µ) and the standard deviation (σ). The mean indicates the center of the distribution, while the standard deviation measures the spread or dispersion of the data points around the mean. A smaller standard deviation indicates that the data points are closer to the mean, while a larger standard deviation indicates a wider spread of data.
Characteristics of Normal Distribution
- The mean, median, and mode of the distribution are all equal.
- About 68% of the data falls within one standard deviation of the mean.
- About 95% of the data falls within two standard deviations of the mean.
- About 99.7% of the data falls within three standard deviations of the mean.
Mean and Standard Deviation Explained
The mean of a normal distribution is a crucial measure of central tendency. In our example, we have a mean of 9.75 meters per second. This average speed indicates that most observations will cluster around this value. To understand the distribution better, we need to look at the standard deviation.
The standard deviation quantifies the amount of variation or dispersion in a set of values. If the standard deviation is low, the values tend to be close to the mean. If it is high, the values are spread out over a wider range. This makes the standard deviation a vital statistic in understanding the reliability and consistency of the data.
Calculating Mean and Standard Deviation
To calculate the mean and standard deviation, you can use the following formulas:
- Mean (µ): µ = (Σx) / N
- Standard Deviation (σ): σ = √(Σ(x - µ)² / N)
Applications of Normal Distribution
Normal distribution has various applications across different fields. Here are some prominent areas where it is utilized:
- Psychology: In psychological testing, normal distribution helps in assessing test scores and identifying outliers.
- Finance: It is used to model stock prices and assess risks associated with investments.
- Natural Sciences: Many natural phenomena, such as heights of individuals, are normally distributed.
Calculating Probabilities in Normal Distribution
Probabilities in a normal distribution can be calculated using the Z-score formula, which helps to determine how many standard deviations an element is from the mean.
The Z-score is calculated as follows:
- Z = (X - µ) / σ
Where:
- X: Value for which you want to find the probability
- µ: Mean of the distribution
- σ: Standard deviation of the distribution
Examples of Normal Distribution in Real Life
Several real-life scenarios illustrate the concept of normal distribution. Here are a few examples:
- Height of Adults: The heights of adults in a specific population tend to follow a normal distribution, with most individuals clustering around the average height.
- Test Scores: Standardized test scores, such as the SAT, often form a normal distribution, making it easier to identify high and low performers.
- Manufacturing: In quality control, measurements of products often follow a normal distribution, helping to identify defects.
Limitations of Normal Distribution
While normal distribution is widely applicable, it is essential to recognize its limitations:
- Not all datasets follow a normal distribution, especially in cases of skewed data.
- Outliers can significantly affect the mean and standard deviation, leading to misrepresentation.
- Assuming normality without testing can lead to incorrect conclusions.
Summary
In summary, normal distribution is a critical concept in statistics characterized by its mean and standard deviation. Understanding these elements allows researchers and professionals to interpret data effectively and make informed decisions. The applications of normal distribution span various fields, including psychology, finance, and natural sciences. However, it is crucial to be aware of its limitations and apply appropriate statistical tests when necessary.
Conclusion
We hope this article has provided you with a thorough understanding of normal distribution, particularly with a mean of 9.75 meters per second and its standard deviation. We encourage you to explore further and apply these concepts in your field of interest. Feel free to leave comments, share your thoughts, or read other articles on our site for more insights into statistics and its applications.
ncG1vNJzZmivp6x7rLHLpbCmp5%2Bnsm%2BvzqZmm6efqMFuxc6uqWarlaR8r7vRppilpKlixKrAx2aYZqWVlrtuu8VmcHBtXaKytbHRrGSpnaJiwKavzqebZpmemXqiedKtmKeckaexbrDEr6CarJmku267xWefraWc