Amplitude refers to the maximum extent of a vibration or oscillation, measured from the position of equilibrium. In physics, the concept of amplitude plays a crucial role in wave theory, especially when discussing wave properties such as frequency, wavelength, and speed. In this article, we will delve into the intriguing topic of "amplitude of 0 m" and explore how constructive interference can be used to generate a wave. This exploration not only enhances our understanding of wave mechanics but also illustrates practical applications in various fields of science and engineering.
Constructive interference occurs when two or more waves meet and combine to produce a wave of greater amplitude. This phenomenon is essential in multiple disciplines, including acoustics, optics, and even in the study of quantum mechanics. By examining the principles behind constructive interference and its relation to wave generation, we can uncover the potential of manipulating wave properties for practical benefits.
In this comprehensive article, we will cover the fundamental concepts of amplitude and constructive interference, their mathematical representations, and real-world applications. We will also touch upon the significance of understanding these principles in various scientific and engineering fields. Join us as we embark on this enlightening journey into the world of waves!
Table of Contents
1. What is Amplitude?
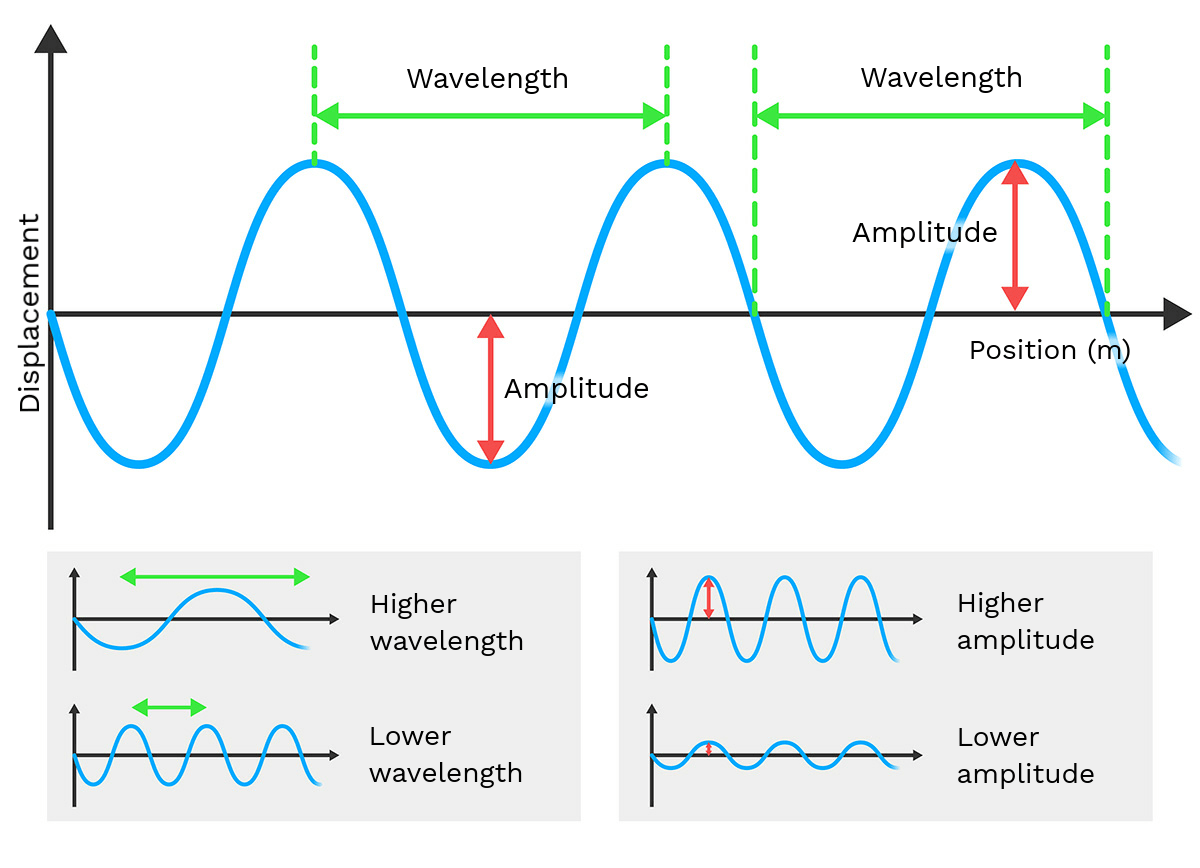
Amplitude is a fundamental property of waves in physics. It refers to the maximum displacement of points on a wave from their rest position. In simpler terms, it is the height of the wave measured from its equilibrium position. Amplitude can be represented in various forms, including:
- Mechanical Waves: In mechanical waves, amplitude is often represented in meters (m).
- Sound Waves: In sound waves, amplitude relates to the volume or loudness of the sound.
- Electromagnetic Waves: In electromagnetic waves, amplitude indicates the intensity of the wave.
When we discuss an amplitude of 0 m, it indicates no displacement from the equilibrium position, meaning the wave is not oscillating. This situation can serve as a baseline for understanding how waves can be generated through constructive interference.
2. Understanding Constructive Interference
Constructive interference occurs when two or more waves overlap in such a way that their amplitudes combine to produce a new wave with a greater amplitude. This phenomenon is characterized by the following:
- Phase Alignment: Constructive interference happens when the peaks (crests) of one wave align with the peaks of another wave.
- Resultant Amplitude: The resultant amplitude is the sum of the individual amplitudes of the waves involved in the interference.
- Applications: Constructive interference is exploited in various technologies, including noise-canceling headphones and laser technology.
Understanding constructive interference is essential for manipulating wave properties, particularly in fields requiring precise control over wave behavior.
3. The Connection Between Amplitude and Constructive Interference
To generate a wave effectively, it is crucial to grasp the relationship between amplitude and constructive interference. Here are some key points to understand:
- When two waves with the same frequency and phase combine, their amplitudes add up, resulting in a wave with a higher amplitude.
- In scenarios where the amplitude is 0 m, waves must be introduced to create constructive interference, effectively generating a new wave.
- By controlling the phase and frequency of the waves, it is possible to optimize the resultant amplitude for desired outcomes.
4. Mathematical Representation of Waves
Waves can be mathematically represented using the wave equation. The general form of a wave function is:
y(x, t) = A sin(kx - ωt + φ)
Where:
- y: Displacement of the wave at position x and time t.
- A: Amplitude of the wave.
- k: Wave number, related to the wavelength.
- ω: Angular frequency.
- φ: Phase constant.
By adjusting the amplitude (A) and the phase (φ), we can explore how changes impact the resulting wave, including the creation of constructive interference patterns.
5. Real-world Applications of Constructive Interference
Constructive interference finds application in numerous fields. Here are some notable examples:
- Acoustics: Sound engineers use constructive interference to enhance sound quality in concert halls.
- Optics: In optical devices, constructive interference is used to create patterns for holography and interference filters.
- Telecommunications: Signal processing techniques leverage constructive interference to improve signal strength and quality.
- Medical Imaging: Techniques such as ultrasound utilize interference patterns to create detailed images of internal structures.
6. Examples of Constructive Interference
To illustrate the concept of constructive interference, consider the following examples:
- Sound Waves: When two speakers emit sound waves of the same frequency and phase, the sound volume increases at certain points in the room due to constructive interference.
- Water Waves: When two waves in a pond overlap while traveling in the same direction, their amplitudes combine, creating larger waves at specific locations.
7. Further Reading and Resources
To expand your knowledge of waves, amplitude, and constructive interference, consider exploring the following resources:
8. Conclusion
In this article, we explored the concept of amplitude, particularly focusing on the scenario where amplitude is 0 m, and how constructive interference can be harnessed to generate waves. We discussed the fundamentals of amplitude and constructive interference, their mathematical representations, and their practical applications across various fields. Understanding these principles is essential for anyone interested in physics, engineering, or technology development.
We encourage you to leave a comment below sharing your thoughts or questions about wave interference. Don't forget to share this article with your friends and explore other insightful articles on our site!
Thank you for joining us on this exploration of waves and constructive interference. We look forward to seeing you again for more engaging discussions and discoveries!
ncG1vNJzZmivp6x7rLHLpbCmp5%2Bnsm%2BvzqZmm6efqMFuxc6uqWarlaR8ornPpaCtrZSaerCyjGlkpmWjnbJur8CnZK6rlWKwsLrSramum6Sew6Z5yKernqqWmr%2BmusKeZK2nXZyyr7HRmqueZZFixKLCxGefraWc