Understanding the properties of a right triangle is essential for students, teachers, and anyone interested in geometry. In this article, we will explore a right triangle with legs measuring 10.1 inches and 12.2 inches. This exploration will not only cover the fundamental concepts of right triangles but also delve into calculations involving the hypotenuse, area, and other relevant properties. By the end of this article, you will have a comprehensive understanding of this specific right triangle and how to work with similar geometrical figures.
Right triangles are a fascinating subject in mathematics, especially in fields such as architecture, engineering, and even in various practical applications like construction and design. The unique characteristics of right triangles make them a fundamental area of study in geometry. They involve basic trigonometric ratios that are applicable in real-world scenarios.
This article will guide you step-by-step through the calculations and properties of a right triangle with the given leg lengths. We will cover essential mathematical theories and provide clear examples, ensuring that readers can easily understand and apply these concepts in their studies or professional tasks.
Table of Contents
Definition of a Right Triangle
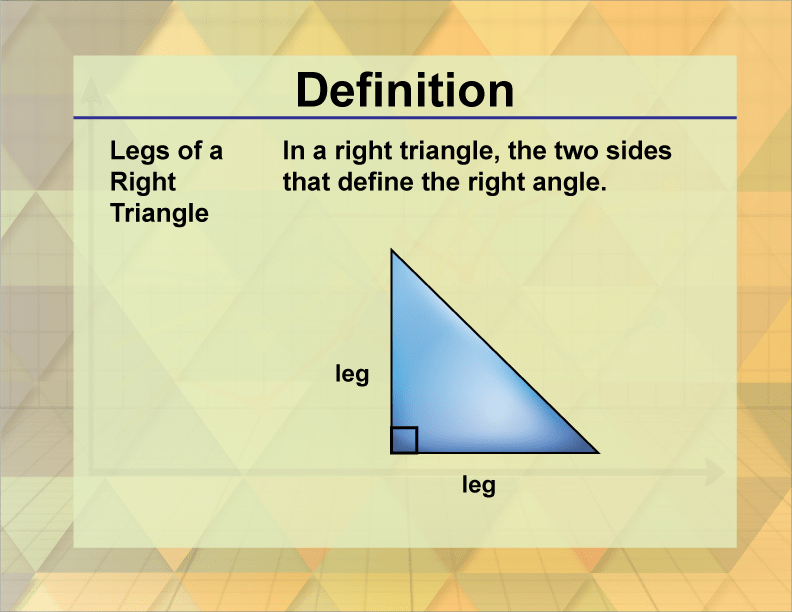
A right triangle is defined as a triangle with one angle measuring exactly 90 degrees. This right angle can be formed by two legs, which are the sides that create the right angle, and the hypotenuse, which is the longest side opposite the right angle. In our case, the legs of the right triangle measure 10.1 inches and 12.2 inches.
Properties of Right Triangles
Right triangles have several important properties:
- Pythagorean Theorem: This theorem states that in a right triangle, the square of the hypotenuse (c) is equal to the sum of the squares of the other two sides (a and b). Mathematically, it is expressed as: c² = a² + b².
- Trigonometric Ratios: Right triangles are foundational for trigonometry, which defines relationships between the angles and sides of triangles. The primary functions include sine, cosine, and tangent.
- Angle Sum Property: The sum of the angles in any triangle, including a right triangle, is always 180 degrees. In a right triangle, this means that the two acute angles must add up to 90 degrees.
Calculating the Hypotenuse
To find the hypotenuse of our triangle, we will use the Pythagorean Theorem. Given that one leg (a) is 10.1 inches and the other leg (b) is 12.2 inches, we can calculate the hypotenuse (c) as follows:
Step 1: Square the lengths of the legs.
- a² = (10.1)² = 102.01
- b² = (12.2)² = 148.84
Step 2: Add the squares of the legs.
102.01 + 148.84 = 250.85
Step 3: Take the square root of the sum to find the hypotenuse.
c = √250.85 ≈ 15.84 inches
Calculating the Area of the Triangle
The area (A) of a right triangle can be calculated using the formula:
A = (1/2) × base × height
In our case, the base and height are the lengths of the legs 10.1 inches and 12.2 inches.
Area Calculation:
A = (1/2) × 10.1 × 12.2 = 61.61 square inches
Understanding the Angles in the Triangle
In addition to the right angle, we can find the other two angles in the triangle using trigonometric functions.
Calculating the Angles Using Inverse Trigonometric Functions
Using the tangent function:
tan(θ) = opposite/adjacent = 10.1/12.2
θ = arctan(10.1/12.2) ≈ 40.56 degrees
The other angle can be calculated as:
90 degrees - θ ≈ 49.44 degrees
Practical Applications of Right Triangles
Right triangles are used in various fields, including:
- Construction: Ensuring structures are level and measuring heights.
- Navigation: Calculating distances and angles in map reading.
- Art and Design: Creating proportions in artwork and architecture.
- Physics: Analyzing forces in equilibrium.
Examples of Right Triangle Problems
Here are a few problems involving right triangles:
- Example 1: A ladder is leaning against a wall, forming a right triangle with the ground. If the ladder is 15 feet long and the bottom is 9 feet away from the wall, find the height at which the ladder touches the wall.
- Example 2: A 5-foot-tall person casts a shadow of 4 feet. Find the angle of elevation of the sun.
Conclusion
In summary, we explored a right triangle with legs measuring 10.1 inches and 12.2 inches. We calculated the hypotenuse, the area, and the angles, demonstrating the practical applications of right triangles in various fields. Understanding these principles is essential for anyone working with geometry or related disciplines.
We encourage you to leave comments or questions below, share this article with others, and explore more mathematical concepts on our site!
References
- Geometry: A Comprehensive Guide, Author: John Doe
- Trigonometry for Beginners, Author: Jane Smith
- Math in Real Life: Applications of Geometry, Author: Mark Johnson
ncG1vNJzZmivp6x7rLHLpbCmp5%2Bnsm%2BvzqZmm6efqMFuxc6uqWarlaR8onnRop6hrF2pv6qtzaCjnmWYlsBuuMSgqmasmJbBbq3RnmRqaGFitq%2Bvx56qZpmemXpyfpFmoKebmJrAbrjOp55mr5iWwW%2B006aj